2908. Просуммировать все

Найти сумму цифр всех чисел от lowerBound до upperBound включительно.

Вход. Каждая строка содержит два целых числа lowerBound и upperBound (0 ≤ lowerBound ≤ upperBound ≤ 2·10⁹).

Выход. Для каждого теста в отдельной строке вывести сумму цифр всех чисел от lowerBound до upperBound включительно.

Пример входа	Пример выхода
0 3 14 53 24660 308357171	6 296 11379854844

РЕШЕНИЕ

динамическое программирование

Анализ алгоритма

Пусть функция f(x) вычисляет сумму цифр всех чисел от 0 до x. Тогда ответом задачи будет значение f(upperBound) – f(lowerBound – 1).

Заведем массив dp[10][11], в котором dp[i][j] равно сумме цифр всех j - значных чисел, первая цифра которых равна i. Изначально положим dp[i][0] = 0. Ячейка dp[0][j] содержит сумму цифр всех чисел, содержащих менее j цифр, то есть сумму цифр всех (j – 1) - значных чисел, начинающихся с любой цифры включая ноль:

dp[0][j] =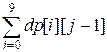

Любое j - значное число, первая цифра которого равна i, образуется из (j – 1) - значного числа приписыванием впереди цифры i. Поэтому сумма их цифр равна сумме цифр (j – 1) - значных чисел плюс цифра i, умноженная на количество j - значных чисел с первой цифрой i (количество последних равно 10^j-1). Получаем соотношение:

dp[i][j] = dp[0][j] + 10^j-1 * i

Остается описать вычисление функции f(x). Очевидно, что f(0) = 0. Пусть x = . Для вычисления f(x) разобьем множество чисел от 0 до x на два подмножества:

1. Числа от 0 до . Сюда входят все (n + 1) - значные числа, начинающиеся цифрой 0, 1, …, a_n – 1. Сумма их цифр равна dp[0][n + 1] + dp[1][n + 1] + … + dp[a_n – 1][n + 1].

2. Числа от 0 до . Цифра a_n в этих числах встречается ( + 1) раз. Сумма остальных цифр этого множества равна f().

Таким образом

f(x) = + a_n * ( + 1) + f()

Реализация алгоритма

Объявим глобальный массив dp.

long long dp[10][11];

Функция info(x, *len, *FirstDigit, *Rest) по входному значению x возвращает количество знаков в числе len, первую цифру числа FirstDigit и число Rest, полученное зачеркиванием первой цифры в числе x.

void info(int x,int *len,int *FirstDigit,int *Rest)

{

int pow10 = *len = 1; *Rest = 0;

while(x > 9)

{

(*len)++;

*Rest = *Rest + (x % 10) * pow10;

x /= 10; pow10 *= 10;

}

*FirstDigit = x;

}

Функция f(x) вычисляет сумму цифр всех чисел от 0 до x.

long long f(int x)

{

int i, len, FirstDigit, Rest;

long long res;

if (x <= 0) return 0;

info(x,&len,&FirstDigit,&Rest);

for(res = i = 0; i < FirstDigit; i++)

res += dp[i][len];

return res + FirstDigit * (Rest + 1) + f(Rest);

}

Функция getSum(lowerBound, upperBound) возвращает сумму цифр всех чисел от lowerBound до upperBound.

long long getSum(int lowerBound, int upperBound)

{

int i, j, k;

Заполняем ячейки массива dp. Значение dp[i][j] равно сумме цифр всех j - значных чисел, первая цифра которых равна i.

for (i = 0; i < 10; i++) dp[i][0] = 0;

for (k = j = 1; j < 11; j++)

{

dp[0][j] = 0;

for (i = 0; i < 10; i++) dp[0][j] += dp[i][j - 1];

for (i = 0; i < 10; i++) dp[i][j] = dp[0][j] + k * i;

k *= 10;

}

Возвращаем ответ.

return f(upperBound) - f(lowerBound - 1);

}

Основная часть программы. Читаем входные данные. Вычисляем и выводим ответ.

while(scanf("%d %d",&lowerBound, &upperBound) == 2)

{

res = getSum(lowerBound,upperBound);

printf("%lld\n",res);

}